Building a Thinking Classroom in Math
Over more than a decade, the author has developed a 14-point plan for encouraging students to engage deeply with math content.
Your content has been saved!
Go to My Saved Content.One day in 2003, I was invited to help June implement problem solving in her grade 8 classroom. She had never done problem solving with her students before, but with its prominence in the recently revised British Columbia curriculum, she felt it was time.
June, as it turned out, was interested in neither co-planning nor co-teaching. What she wanted from me was simply a collection of problems she could try with her students. The first one I gave her was a Lewis Carroll problem that I’d had much success with, with students of different grade levels: If 6 cats can kill 6 rats in 6 minutes, how many will be needed to kill 100 rats in 50 minutes?
June used it the next day. It did not go well. A forest of arms immediately shot up, and June moved frantically around the room answering questions. Many students gave up quickly, so June also spent much effort trying to motivate them to keep going. In general, there was some work attempted when June was close by and encouraging the students, but as soon as she left the trying stopped. This continued for the whole period.
The following day I was back with a new problem. The results were as abysmal as they had been on the first day. The same was true the third day. Over the course of three 40-minute classes, we had seen little improvement in the students’ efforts to solve the problems, and no improvements in their abilities to do so. So June decided it was time to give up.
I wanted to understand why the results had been so poor, so I stayed to observe June and her students in their normal routines. After three full days of observation, I began to discern a pattern. That the students were lacking in effort was immediately obvious, but what took time for me to realize was that the students were not thinking. More alarming was the realization that June’s teaching was predicated on an assumption that the students either could not or would not think.
Once I realized this, I proceeded to visit 40 other mathematics classes in a number of schools. In each class, I saw the same thing—an assumption, implicit in the teaching, that the students either could not or would not think. Under such conditions it was unreasonable to expect that students were going to be able to spontaneously engage in problem solving.
This motivated me to find a way to build, within these same classrooms, a culture of thinking. I wanted to build what I now call a thinking classroom—one that’s not only conducive to thinking but also occasions thinking, a space inhabited by thinking individuals as well as individuals thinking collectively, learning together, and constructing knowledge and understanding through activity and discussion.
Over 14 years, and with the help of over 400 K–12 teachers, I’ve been engaged in a massive design-based research project to identify the variables that determine the degree to which a classroom is a thinking or non-thinking one, and to identify the pedagogies that maximize the effect of each of these variables in building thinking classrooms. From this research emerged a collection of 14 variables and corresponding optimal pedagogies that offer a prescriptive framework for teachers to build a thinking classroom.
1. The type of tasks used: Lessons should begin with good problem solving tasks. In the beginning of the school year, these tasks need to be highly engaging, non-curricular tasks. Later these are gradually replaced with curricular problem solving tasks that then permeate the entirety of the lesson.
2. How tasks are given to students: As much as possible, tasks should be given verbally. If there are data, diagrams, or long expressions in the task, these can be written or projected on a wall, but instructions should still be given verbally.
3. How groups are formed: At the beginning of every class, a visibly random method should be used to create groups of three students who will work together for the duration of the class.
4. Student work space: Groups should stand and work on vertical non-permanent surfaces such as whiteboards, blackboards, or windows. This makes the work visible to the teacher and other groups.
5. Room organization: The classroom should be de-fronted, with desks placed in a random configuration around the room—away from the walls—and the teacher addressing the class from a variety of locations within the room.
6. How questions are answered: Students ask only three types of questions: proximity questions, asked when the teacher is close; “stop thinking” questions—like “Is this right?” or “Will this be on the test?”; and “keep thinking” questions—ones that students ask in order to be able to get back to work. The teacher should answer only the third type of question.
7. How hints and extensions are used: The teacher should maintain student engagement through a judicious and timely use of hints and extensions to maintain a balance between the challenge of the task and the abilities of the students working on it.
8. Student autonomy: Students should interact with other groups frequently, for the purposes of both extending their work and getting help. As much as possible, the teacher should encourage this interaction by directing students toward other groups when they’re stuck or need an extension.
9. When and how a teacher levels their classroom: When every group has passed a minimum threshold, the teacher should pull the students together to debrief what they have been doing. This should begin at a level that every student in the room can participate in.
10. Student notes: Students should write thoughtful notes to their future selves. They should have autonomy as to what goes in the notes and how they’re formatted. The notes should be based on the work already on the boards done by their own group, another group, or a combination.
11. Practice questions: Students should be assigned four to six questions to check their understanding. They should have freedom to work on these questions in self-selected groups or on their own, and on the vertical non-permanent surfaces or at their desks. The questions should not be marked or checked for completeness—they’re for the students’ self-evaluation.
12. Formative assessment: Formative assessment should be focused primarily on informing students about where they are and where they’re going in their learning. This will require a number of different activities, from observation to check-your-understanding questions to unmarked quizzes where the teacher helps students decode their demonstrated understandings.
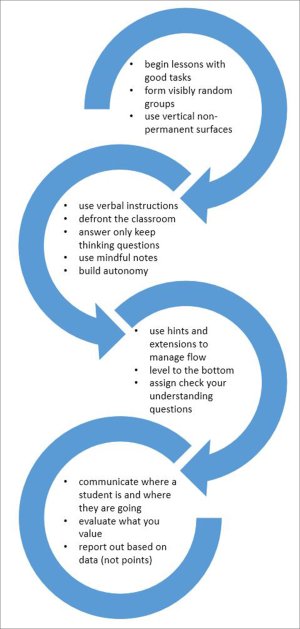
13. Summative assessment: Summative assessment should focus more on the processes of learning than on the products, and should include the evaluation of both group and individual work. Summative assessment should not in any way have a focus on ranking students.
14. Reporting out: Reporting out of students’ performance should be based not on the counting of points but on the analysis of the data collected for each student within a reporting cycle. The data need to be analyzed on a differentiated basis and focused on discerning the learning a student has demonstrated.
My research also shows that the variables and accompanying pedagogical tools are not all equally impactful in building thinking classrooms. And there is an optimal sequence for both teachers and students when first introducing these pedagogies. This sequence is presented as a set of four distinct toolkits that are meant to be enacted in sequence from top to bottom, as shown in the chart. When these toolkits are enacted in their entirety, an optimal transformation of the learning environment has been achieved in the vast majority of classrooms.
