Advanced Level Projects with Scratch: Fun with Fractals

In his book Program or Be Programmed, author Douglas Rushkoff describes computer programming as an essential literacy for the 21st century. It makes sense, as we recognize the importance of teaching students to communicate by listening and speaking, and we go to great lengths to teach reading and writing. Now, in an increasingly digital world, we should ensure that our students have experience using and making programs.

In our previous tutorials about elementary and intermediate level Scratch, we practiced programming by using code to draw 2D geometric shapes commonly covered in elementary mathematics curriculums. Now we’ll address middle and high school level material with a new problem-solving strategy called recursion, a central idea of computer science.

There is an interesting example of recursion found in nature called a fractal. Fractals are repeating patterns that look similar at every scale of magnification. We’ll teach our computers to draw a famous fractal -- the Sierpiński Triangle. If you prefer video guides you can watch the tutorial instead.

Here's How

A Quick Review

• Visit scratch.mit.edu.
• If you haven't already, sign up for an account by clicking on "Join Scratch" at the top right of your browser window. This isn't required to actually use Scratch, but it's necessary if you want to save your work.
• Click the "Create" button near the top left of your browser window to start a new project.
• In our beginner tutorial, we got to know the layout of the Scratch interface. Check it out if you need a primer on the four main areas of the program: the Stage, Sprite List, Palette, and Scripts Area.

1st Challenge: Basic setup and variable creation.

• Delete the default Cat sprite by selecting the Scissor tool  in the Sprite Toolbar at the top of the interface and then clicking on the Cat sprite to remove it.
• Now add the "Ladybug1" sprite by clicking "Choose Sprite from Library" in the Sprite List. (Any sprite will do.)
• Click on the "Data" section of the Palette and then click the "Make A Variable" button.
• Name your variable "Size".
• Click OK to continue.
• Make three more variables and name them "Levels", "CenteredX", and "CenteredY".
• Think of a variable as simply a container for a value. For example, a scoreboard has variables that contain points.

2nd Challenge: Make three custom blocks for drawing fractal art.

The "Make A Block" feature allows you create custom procedures that you can reuse in your Scratch projects. We'll need three custom blocks for this project. Here's how to make a custom "triangle" block:

• Click on the "More Blocks" palette and then click the "Make A Block" button.
• Type "triangle" in the field to name the block.
• Click the "Options" text drop-down arrow.
• Click "Add A Number Input".
• Type "size" to replace "number1". This number will set the side length of each triangle drawn. Programmers call these input definitions "parameters".
• Click OK to continue.
• Add the code blocks below to your new "triangle" procedure:

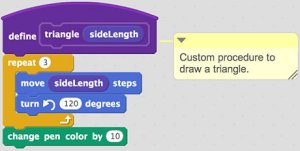
How It Works

Taking a cue from our first tutorial, this new block contains a custom procedure for moving in a triangular pattern enabling equilateral triangles to be drawn.

Make a "Sierpiński" block.

• Make a second block named "Sierpiński".
• Click the "Options" text drop-down.
• This time, make two number inputs.
• Name one "sideLength" and the other "levelOfRecursions".
• Click OK to continue.
• Add the code blocks below to your new "Sierpiński" procedure.

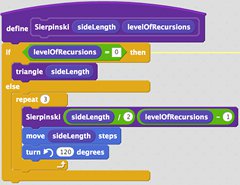
How It Works

We've just defined a new procedure named Sierpiński, and it takes two inputs called "sideLength" and "levelOfRecursions". (We'll prompt the user for these two numbers when the program is run.) Basically, this function uses an algorithm to draw an intricate pattern of self-similar triangles named after Wacław Sierpiński, the Polish mathematician who first described it in 1915. You'll also notice something unusual: there is a Sierpiński block inside the definition of the Sierpiński procedure itself. This technique is called recursion, a powerful method for problem solving by repeating commands. It can be tricky to understand at first, but you'll find that recursion can provide an elegant solution to many computer science problems.

We can follow the flowchart below to demonstrate how Sierpiński works when it is called with a "levelOfRecursions" argument of 1:

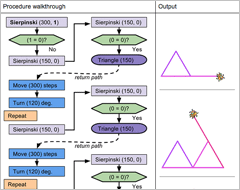
The procedure starts with user input of 1 level of recursion and a largest triangle side length of 300 pixels. The procedure first checks if "levelOfRecursions" is equal to 0. Since 1 is not equal to 0, the procedure subtracts 1 from "levelOfRecursions" and calls itself with an argument of 0. The "Move" and "Turn" blocks are not yet reached and nothing is drawn on the Stage.

In the second call, "levelOfRecursions" does equal 0, executing a call to the "triangle" procedure, which draws a triangle with a side length of 150 pixels. The procedure returns to the "Move" and "Turn" blocks from the first call, moves 300 pixels, and turns 120 degrees. This process is repeated three times total as required by the "Repeat" loop inside the "Else" statement, drawing two more triangles of 150 pixels at different positions on the Stage.

Make a “centerTheDrawing” block.

• Make a third block named "centerTheDrawing".
• Click the "Options" text drop-down.
• Click "Add a Number Input".
• Type "sideLength" to replace "number1".
• Add the code blocks below to your new "centerTheDrawing" procedure:

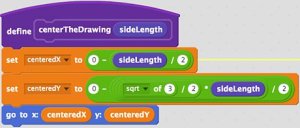
How It Works

• The next custom procedure centers the entire drawing on the Stage by calculating the appropriate starting position for the Sprite based on the user's desired size input. The Sierpiński procedure draws the fractal in a spiraling, counter-clockwise pattern from the bottom left corner of the largest triangle.
• The Stage is a four-quadrant coordinate grid with the origin (0, 0) in the center. The X limits are 240 and -240, and the Y limits are 180 and -180.
• So if we know the Stage has a center point of X = 0, then to center the triangle horizontally drawing should start at centeredX = "0 - sideLength / 2". We're considering the base of this triangle to be its width.
• To find the vertical center, we first need to find the height of the equilateral triangle because it's not the same as the length of its sides. That formula is height = (√ 3  / 2) sideLength. Now that we know its height, we can center the triangle drawing vertically by calculating centeredY = "0 - height / 2"

3rd Challenge: Write the main code sequence below to make the bug draw fractal triangles based on user input.

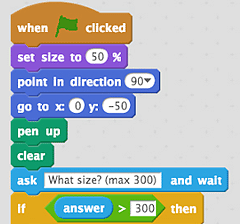
• If the user inputs a number greater than 300, then we set the "Level" variable to 6 anyway, and use the "Think" block to give the user some feedback about the limit.
• Else the user has input a valid number, and we set the "Level" variable to the user's input.

Sit back and enjoy some eye-catching, animated mathematical art!

Wrapping Up

This has been our richest computational thinking activity so far, covering principles like sequences, events, loops, operators, conditionals, functions, and data. Most notably, we've introduced recursion -- an important problem-solving technique in computer science.

If you're looking to dive deeper, please explore some other Scratch educator resources:

• Here's a great resource on teaching with fractals from Cynthia Lanius of Rice University and the EL Computing Scholars of Tomorrow Alliance.
• Check out some Scratch studios with collections of fractal-based projects:
  • The Fractal Gallery
  • The Ultimate Fractal Gallery
  • My Fractal Collection