Mathematical Habits of Mind
Your content has been saved!
Go to My Saved Content.We all have them, some good and some bad. We pick them up from friends, family, and even strangers. But we may not recall who we picked them up from or when they began.
Because we've practiced them over and over, these seemingly thoughtless repeated habits or behaviors, the pathways in our brain have become so broad, fast, and efficient in carrying them out that we do them automatically without even thinking. Yet these unconscious habits and behaviors add structure and order to our lives and help us to make sense of the world we live in.
Our classrooms are full of them. We teachers are pros when it comes to employing and modeling good habits and routines that enable us to manage and carry out the many tasks and demands of teaching. And when it comes to teaching mathematics, we model and teach our students how to carry out procedures and algorithms flawlessly. But why is it that these same students often struggle when confronted with a problem to which the immediate answer is unknown?
Experienced vs. Inexperienced Problem Solvers
According to Levasseur and Cuoco (PDF, 80KB), it's the mathematical habits of mind, or modes of thought, that enable us to reason about the world from a quantitative and spatial perspective, and to reason about math content that empowers us to use our mathematical knowledge and skills to make sense of and solve problems. It's these habits that separate the "experienced" from the "inexperienced" problem solver.
Far too many students can be classified as inexperienced problem solvers who don't know what to do when they don't know what to do. These are the students who lack experiences in making sense of and solving problems, and in communicating and using precise, appropriate mathematics and mathematics language. They have never developed the overarching habits of a productive mathematical thinker.
When they're presented with a problem to which they don't know the immediate answer, their bad habits often rise to the occasion. They may begin with no real strategy in mind, they look for key words and terms that can sometimes be misleading, they want a quick answer, they resort to memorization over understanding, or they simply make no effort at all in finding the solution to the problem.
On the other hand, experienced problem solvers know what to do when they don't know what to do! They practice perseverance and automatically employ the mathematical habits of mind of a productive problem solver in their quest for a problem solution. They automatically engage in Polya’s four-step problem-solving process to find a solution to the problem.
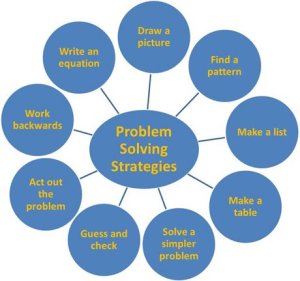
No one has to remind experienced problem solvers to first make an attempt at understanding the problem and ask clarifying questions that help them interpret and understand the conditions of the problem. They instinctively try to make sense of the mathematical situation at hand and choose a strategy, tools, and/or models, often based upon previous learning experiences or problems they've solved -- experiences that they see as relevant and applicable in solving the problem.
If they try a strategy and it doesn't work, they try a different one – all part of perseverance in problem solving. And like any good problem solver, once they have a solution, they take one last look to determine if their solution is a reasonable solution to the problem.
Practice and Experience
But these habits of mind can’t be learned and developed by simply talking about them or memorizing the definition. Students immersed in classroom experiences that let them engage in learning mathematics concepts through problem solving, making and using abstractions, and developing and applying mathematical theories have greater opportunities for developing mathematical habits of mind. Classrooms steeped in the Common Core Standards for Mathematical Practice (MP) provide maximum opportunities for students to learn and develop these habits as they:

Teachers who saturate learning experiences with the Standards for Mathematical Practice offer students a variety of palatable problems. Presenting relevant, interesting, and challenging problems that can be approached and solved with different strategies and tools gives students choices that best fit their learning preferences. This approach is more inviting to them and leads them to reason about, look for, and make use of structure. In turn, it increases their chances of understanding important math concepts and skills, which in turn increases their ability to explain their thinking and reasoning, and to critique the reasoning of others.
You play a vital role in the development of mathematical habits by conveying to your students a mindset that fosters productive struggle and emphasizes the possible value of wrong answers. You set the stage by embracing the importance and value of grappling with problems. The more you engage your students in learning and doing mathematics, the greater the likelihood of their developing the mathematical habits of mind of a productive mathematical thinker -- and becoming experienced problem solvers who know what to do when they don't know what to do.