Building Students’ Number Sense in Elementary Math

In my second-grade math classroom, I typically teach measurement and then teach a unit focusing on addition and subtraction on the number line. The goals of the unit include exploring the structure of the number line and learning how to use it for addition and subtraction within 100. The heart of this unit is exploration of the number line as a vehicle for building number sense.

Number sense is essentially how it sounds—our internal sense of numbers. According to Christina Tondevold of Build Math Minds, this includes their relationships to each other, the magnitude of numbers, estimation, and our ability to visualize varying amounts. The number line can help students construct their own understanding and sense of numbers, while also providing a context for rich discussion that can engage all learners. My goal is for students to develop a visual feel for distances between numbers, one that is based on reasoning rather than memorized facts.

Starting Off the lesson

The lesson started with a strip of paper taped to the whiteboard at the front of my classroom. One end was labeled with “0” and the other end was “30.” While we had spent time exploring a physical number track, with a space for every number, this was the first time that students were working with a more open number line. I wanted to ensure that the task was within everyone’s Zone of Proximal Development, so everyone could engage with it.

I handed out some thin sticky notes with the following numbers written on them: 4, 8, 11, 18, 21, 26, and 29. Students were then asked to place their sticky notes on the number line, wherever they thought they belonged. My students love coming up to the board, so they didn’t hesitate to start placing their numbers.

Once all the numbers were placed, we paused and observed. I asked my class, “Do you agree with all the numbers, or are there any that you disagree with?” Hands went up and the discussion began. 

At first, comments and questions focused narrowly on the minutiae of how much is between two numbers, rather than seeing the big picture of the entire number line. They thought that 4, 8, and 11 were too close together, because “you need space for 5, 6, and 7” but not because 0 and 4 have the same distance as 4 and 8. The number 18 was also closer to 0 than it was to 30!

Looking at the Big Picture

At this moment, I wanted my students to look at the number line as a whole, starting with 0 and 30 as the range. I asked what number they thought would go in the middle. Some students knew that it was 15 and were able to explain why, which brought up our first connection: A student asked how it could be 15 when 30 was an odd number. A misconception to address!

To help make the concept more concrete for everyone, I had students work with ten frames. Three ten frames went on the board, and a student started to split 30 into two equal groups, while I wrote what they were doing on the board, within a number bond. Soon, we were able to see that even though the digit 3 is an odd number, 30 actually means 3 tens, and 10 is an even number, so 30 is an even number! We can split 30 into two equal groups. With excitement, a student called out, “Wait, are we doing division?” Indeed we were.

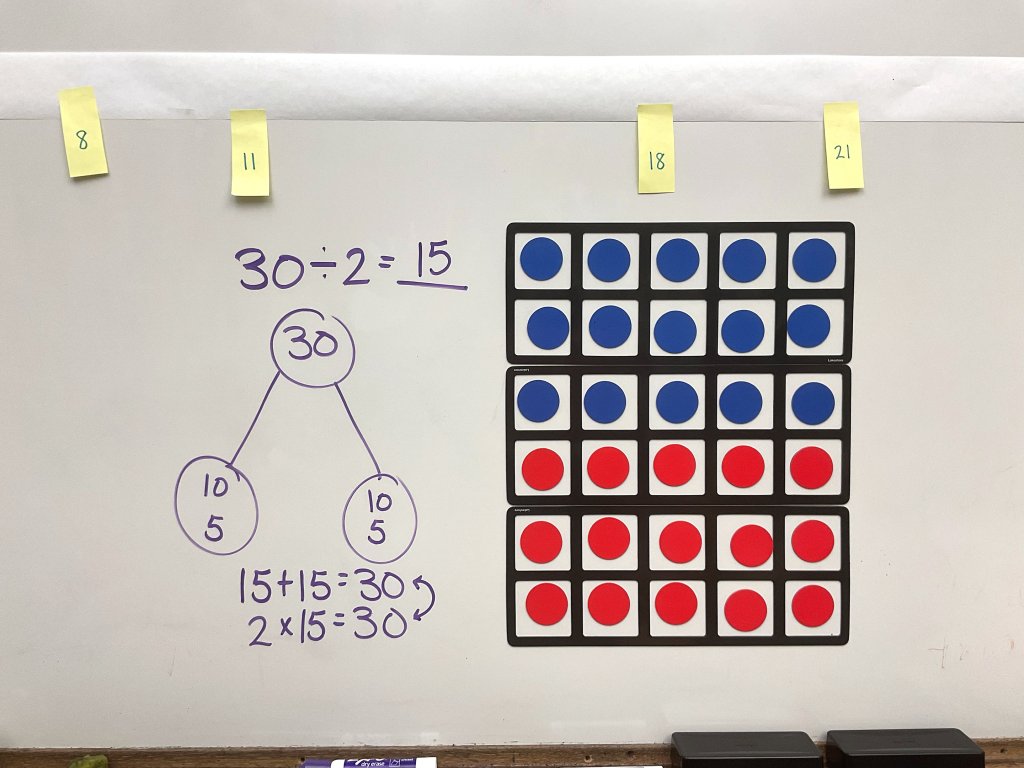
We then added 15 to our number line and discussed two vocabulary terms: benchmarks, commonly called “friendly numbers”—we defined benchmarks as the two ends of the number line; and the midpoint, the exact middle of two benchmarks. I gave my students a chance to adjust the numbers, based on our new information. Pro tip: You have the best view of the number line if you’re standing farther away from it, straight back. I often like to assign a student sitting in the center back of the room with the job of checking my work.

Encouraging Productive Struggle

Next, we focused on 4, 8, and 11 and noticed that 4 and 8 were really close together, but 0 and 4 were farther apart. We discussed the distance between 0 and 4, then 4 and 8, and realized they were the same distance apart, so that needed to be reflected on the number line. Those numbers also needed to be farther apart than 8 and 11, but not by much.

We repeated this conversation, with decreasing teacher support, for the other half of the number line. Students continued to adjust the numbers and practiced explaining their thinking and defending their answers. They continued making the number line better and better until they were completely satisfied with their work.

Modifying the Lesson for the Elementary Grades

This is just one example of a deep dive into a number line. We kept coming back to this task—placing a set of numbers on a number line—with different endpoints (including starting at a number other than 0) and different distances between endpoints. The more number lines we worked with, the more independent my students became. Soon, they were integrating new vocabulary terms and estimating distances between numbers to form arguments on the placement of new numbers. 

While this example is from a second-grade class, this activity could easily be modified for any elementary classroom:

• First graders can place whole numbers within a decade—for example, between 0 and 10.
• Third graders can work with larger and longer number lines, especially as a precursor to rounding.
• Fourth and fifth graders can explore number lines with fractions and decimals—between 0 and 1.

I believe that number sense building activities should be a part of our students’ day, every day, just as read-alouds are a part of every day. Number lines are one of many valuable tools for mathematical thinking. They can be part of a regular number sense building routine in your math class, but because of the emphasis on discussion and collective understanding, they also would be a valuable addition to your morning meeting. Your students will be thinking and talking math before you know it!