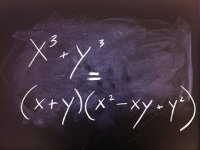How to Teach Kids About Factoring a Polynomial
Your content has been saved!
Go to My Saved Content.Recently, I applied to a fellowship with Math for America, a program dedicated to improving mathematics education in U.S. public schools by recruiting, training, and retaining highly qualified secondary school math teachers. In my quest to get the fellowship, I started to fiddle around with some math ideas that made me curious. One of those is the idea of factoring a polynomial, and specifically, how we teach it.
For one, I'm not a fan of FOIL (first-outside-inside-last) for a plethora of reasons. While I think it's handy to have an acronym that reminds students of a procedure, it only works in a very special case. In this case, FOIL works only for multiplying a binomial by another binomial. Does FOIL lead students toward understanding multiplication of all types of polynomials, or understanding why the distributive property works even with variables? I'm not so sure.
We do know that there are alternate ways of approaching multiplication of binomials, but I'd like to focus on using the geometric method of multiplication because, well, because I can.
Multiplication and Factoring Using Areas
Multiplying (x + 2) by (x + 3) can be represented like so (see Figure 1):
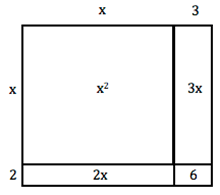
This makes the following operations look rather simple:
(x + 2)( x + 3)
x 2 + 2x + 3x + 6
x2 + 5x + 6
Using the area method for multiplying binomials also makes factoring an easy task. We can visualize the squares and rectangles in this shape while thinking to ourselves, "Which two numbers have a sum of 5 (second term) and a product of 6 (third term)?" If we look carefully, students have another method for understanding why we get the terms we do after multiplying the binomials shown. How does this relate to trinomials? Let's see.
Multiplication and Factoring of Cubes
Let's take the last example and multiply it by (x + 4). Like so (see Figure 2):
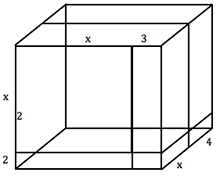
(x + 2)(x + 3)(x + 4)
(x2 + 5x + 6)(x + 4)
x3 + 9x2 + 26x + 24
Or geometrically (see Figure 2): This has awesome implications for finding both the surface area and volume of this figure. Since we already figured out the "face" of this cube earlier (x2+ 5x + 6), we're basically multiplying that face by the length of x and by the length of 4. This yields:
x(x2 + 5x + 6) + 4(x2 + 5x + 6)
. . .
x3 + 9x2 + 26x + 24
Factoring The Cube
Once we find the quadrinomial, the cube gives us a hint for finding the lengths that created the quadrinomial. One would only need to figure out which three numbers give us a sum of 9 (second term) and a product of 24 (last term). These numbers are 2, 3, and 4, so we'll get (x + 2)(x + 3)(x + 4).
Is this much better than using the cubic formula? Absolutely, especially for our students.
What about a quadrinomial like 2x3 - 11x2 + 12x + 9? We can try to determine all the real roots of this polynomial, or we can take a look at the second and last terms. The simplest combination for a product of 9 is multiplying 3, 3, and 1. The first term's coefficient, 2, makes getting a -11 tricky. We can't get -11 from the set of numbers without considering the first coefficient.
Yet, as we've seen with the other cubes (see Figure 3):
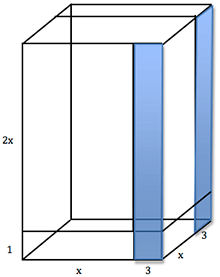
We will see that the term of 2x will multiply with any lengths that aren't associated with it. Thus, (2x - 3) + (2x - 3) will give us 6x + 6x, or 12x. Since we needed to get -11x, this means the remaining 1x is positive and the 12x is actually -12x.
Therefore, our quadrinomial gets factored to (x - 3)( x - 3)(2x + 1) or (x - 3)2(2x + 1).
Word of Caution
I'm still exploring this for other cases (looking at x3 + 27, for example), and what imaginary numbers would look like using this model. These methods work great as a way to draw students in, but some special cases will probably require more space than I could lend it here.
Also, this was my rebellion against the cubic formula which, as many mathematicians know, makes little sense to introduce in the classroom.
Let me know what you think in the comments below.