Highlighting ‘Good’ Mistakes in Student Work

As I was grading my class’s algebra quizzes, I noticed that a conceptual error kept appearing on multiple students’ papers. I pulled out my phone and snapped photos of various students’ solutions—some with mistakes, some without. The next day in class, I displayed selected photos as a guide to start a whole-class conversation about the various solutions. (The identities of the students whose work was displayed were not revealed to the class.)

Here are some of the responses from the eighth graders as we viewed the photos: 

• “Oh, I see how they used the equation from the table of values to identify the slope.” 
• “Why did they multiply 0.5 by 14? I did something different.” 
• “Yes, I see the mistake there. They assumed the y-intercept was zero.” 
• “I like how they showed the common difference in the table.” 

Why share photos of student work? All of the above student comments about the sample of student work contributed to the learning of the concept. I could have re-created each student’s solution on the board; however, students benefit from seeing each other’s work rather than only the teacher’s. 

Katrina Schwartz writes in the 2014 KQED article “How Looking at Student Work Keeps Teachers and Kids on Track,” “Examining and critiquing student work as a regular part of classroom interactions can be a powerful way for both teachers and students to reflect on their work, while building a community culture that focuses on the process of learning.” When multiple students’ or groups’ work samples are shared in a planned sequence, the whole class can make connections between the mathematical concepts that may not be achieved by seeing only their own work.

Expecting and Respecting Mistakes

While discussing photos of student work provides an opportunity for achieving the Common Core standard of “critiquing the reasoning of others,” it’s crucial to keep the environment supportive and encouraging for all students. Teachers can foster such a culture by acknowledging “good mistakes.” Read more about ways to create a mistake-friendly classroom in Meghan Laslocky’s 2021 Edutopia article “The Mistake-Friendly Classroom.” 

What if a student does not want their work shared? 

Yes, even though the identity of the student is not revealed, another classmate might recognize the handwriting. This is why it’s imperative to establish a class culture of collegial encouragement and respect. I would never display egregious mistakes that would run the risk of embarrassing a student if their identity were  known. The teacher can preface the student work sample with “This was a common error; however, I chose this sample because they clearly started off with the correct approach. Let’s discuss how we can learn from this example.” 

While students are working in groups at their desks, snap photos that will kick off a meaningful class discussion. I ask the student if they would be willing to discuss their work with the class. If they would rather not, I ask if it’s OK for another student to come to the board to interpret and explain the process and steps. When one student explains another student’s work, both the explainer and the solver practice clear mathematical communication. 

If students are working at the whiteboards in groups (also referred to as vertical non-permanent surfaces, or VNPS, in Peter Liljedahl’s book Building Thinking Classrooms in Mathematics), then everyone can see the group’s work if you have them present or take a gallery walk. Occasionally, I deem a group’s work worthy of future reference, and I snap a photo for the other sections to see (otherwise, the whiteboard work will be erased and never seen again).

In an article in Mathematics Teaching in the Middle School, “Examining Mistakes to Shift Student Thinking,” the authors suggest displaying mistakes that are “worthy” of discussion. Worthy mistakes can be computational, conceptual, or procedural in nature. A worthy mistake will deepen the understanding of the mathematical goal of the lesson for all students—not just the one who made the error. 

Desmos Classroom, a free online graphing calculator website that also includes digital activities, has a feature that enables teachers to snapshot student responses during an activity. By adding these snapshots to an album, the teacher can display students’ work side by side to spark a discussion about student thinking. There is a field at the top of the presentation screen to ask the class a guiding question about the displayed student work. (Desmos also features an “anonymize” option to display student names as famous mathematicians‘ names.)

Below is an actual example of a photo I used in my algebra class. (The student’s identity was not shared with the class.) This image led to a discussion of the multiple methods to compare an equation and table of values. Many students struggled with this problem on their assessment for many different reasons. My goal was to share a sample of how to interpret a table of values as an equation.  

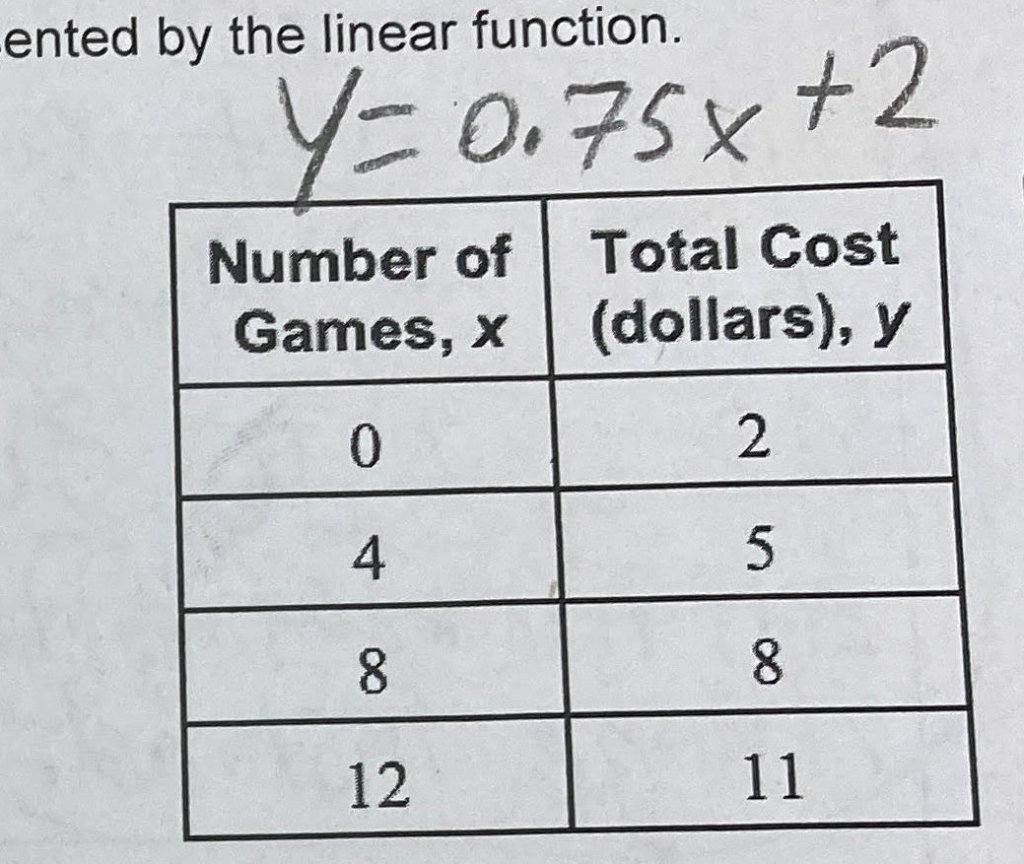
First, I asked the class what they noticed about the equation written above the table. “How did they calculate the slope and y-intercept? What communication could be added here to clearly communicate the calculation of the slope?” At this point, a student might come to the board to annotate the table with common difference or the slope formula.

The side arithmetic could also lead to an interesting discussion about calculating decimals; however, because this was not the focus of the lesson, I did not follow that path of a potential conversation. 

As you teach your math classes, keep your eyes open to samples of student work that could further the understanding of the lesson. These images could be taken from both formative and summative assessments such as homework, classwork, group work, exit tickets, and/or quizzes/tests.

To curate which photos are best for the whole class discussion, consider which mistakes are discussion worthy. I frequently announce during these discussions, “This is my favorite mistake!” Then follow up with how the mistake helps everyone in the class gain a better understanding of the concept.