Programming & Simulation: Real Technical Skills for Today’s Student

Technology is here to stay. There are two main ways of interfacing with technology: passively as a user and actively as a developer. Today's technical problems are very complicated -- they cannot all be solved in theory on a whiteboard or exhaustively via computation. The use of simulation methods to obtain a "solution" to the problem at hand is not uncommon in industry. The purpose of this post is to provide broadly a "why" and "how to" for introducing simulation methodologies into high school math and programming courses. While the subject matter is technically deep, the concepts are well within the grasp of high school students -- and possibly younger students.

A Quality Control Example

In practically every industry, there is heavy pressure to cost-effectively produce high quality products. The quality control processes in place can vary depending on the rules and regulations, the business impact of a faulty product making it to market, the quantity of the product being produced, etc.

So let's say that we run a widget-making business. Our widgets are complex and require ten independent components to be fitted together for the widget to work. If one component is faulty, the widget won't work. Fortunately, we can test each component with 100% accuracy before assembling it into the widget. We build widgets on demand and thus we are not concerned with excess capacity. Each component, inclusive of all expenses, costs one dollar to manufacture. So at minimum, each widget costs us ten dollars. We sell each widget for twelve dollars.

If we manufacture each component with 99% efficiency, are we making or losing money on our widgets?

If we can simulate producing, say, one million widgets with the rules stated above, we could get an idea for the average cost, among other things.

Here is what code (with overly verbose variable names) could look like. This is written in a programming language called Python.

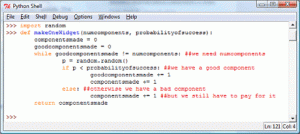
And here is what happens if we run a few instances of it. As we can see, it looks like we use ten components to make a widget.

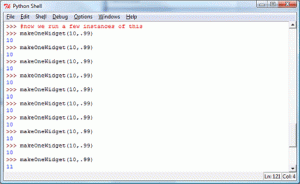
But! We have computing resources at our disposal. So let's see what happens to our average cost if we make one million widgets.

And voila, it's as easy as this:

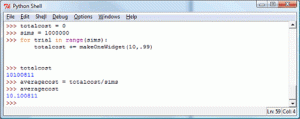
As we can see, it looks like our average cost is $10.10 per widget. Which means that each component really costs us on average $1.01. We certainly are making money. (What's our profit margin?)

What would happen to our cost if we could only test our widget once we had all ten components together? And since we've built the widget, if it is faulty we have to toss the entire widget. Are we still profitable? I will leave this as an exercise for the reader.

The creative instructor can also add several other exercises that build on this. What happens to the cost of a widget if our efficiency goes to, say, 98%? Also, would the cost of producing a component decrease if our efficiency decreased? What are the business ethics of this? The instructor can also discuss topics like statistical error (we probably can't have a 100% effective test), independence of events, standard deviation/standard error, etc.

Other Exercises to Consider

In the previous section, we saw how a simple and graspable problem of quality control is rich in lessons about probability and programming. Additionally, while a student may have difficulty solving this problem on paper, it can be readily tackled via a few short programs. Here are some exercises that the instructor may want to consider:

• The Travel Industry Problem: What is the cost/benefit of overbooking for airlines and hotels?
• The News Vendor Problem: How many newspapers should the news vendor print?
• The Traveling Salesman Problem: What is the most cost-efficient tour of cities? (This can be a nice classroom competition!)

Getting Started

I took programming in high school and as an undergraduate. I didn't understand programming one bit. Then at my first post-bachelor's degree job, I wanted to automate some spreadsheet task, and suddenly, for reasons unknown to me, programming was not difficult. I've never looked back since, and I continue to learn about the new technologies out there. If it weren't for that exposure early on, the information would never have marinated in my brain, and the time it would have taken me to learn how to program would have been much greater -- time that my job probably could not have afforded.

If you're interested in pursuing activities like these, here are some classroom tips:

• It's not synchronized swimming. Not everyone is going to learn at the same pace.
• Some students will ask to see many examples before they feel that they've mastered the subject.
• Some students will feel comfortable editing code at first before writing from scratch on their own.
• Have students comment, line by line, on small snippets of code that you have written.
• Some students may simply not understand. Instead of expecting that they will learn how to program through a specific programming language, try to engage them in algorithmic and procedural thinking outside of mathematics and programming.